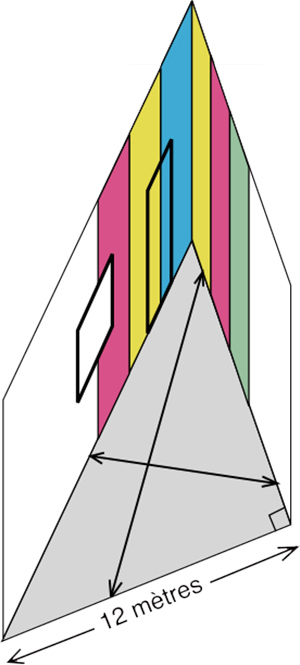
Le cahier des charges d'un immeuble de bureaux prévoit que l'un des locaux à louer doit être un atelier d'artiste. Ce local, contrairement aux autres, est constitué d'une seule pièce en forme de triangle rectangle isocèle dont les côtés de l'angle droit ont une longueur de 12 mètres, et qui ne comporte aucune cloison intérieure. L'artiste qui vient de louer ce local est passionné par les couleurs. Il a décidé de peindre les murs de son atelier en bandes de couleur verticales, sur toute la hauteur des murs, en utilisant exactement quatre couleurs. Il voudrait également que deux points des murs distants de plus de 7 mètres, mesurés horizontalement (au niveau du sol par exemple), ne soient jamais de la même couleur.
Montrez que c'est impossible. On ne tiendra pas compte des portes (qui sont supposées être peintes), ni des fenêtres.