
Le théorème de Thalès n'est pas forcément celui que l'on croit. Euclide avait sa version, démontrée proprement, sur le lien entre angle inscrit et angle au centre. Leurs successeurs géomètres ont abondamment utilisé leurs résultats, qui en ont engendré d'autres, et les artisans les ont appliqués à leurs tracés. C'est ainsi que l'angle au centre et son double, l'angle inscrit, sont entrés dans l'histoire des mathématiques.
L'autre théorème de Thalès
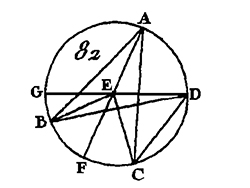
Figure tirée de l'édition Louis de 1804 des Éléments d'Euclide (traduction de François Peyrard).
Astronomes, arpenteurs et géomètres ont, très tôt, cherché à mesurer des angles et à les comparer entre eux. Dans l'ancienne Égypte, vers 2500 avant notre ère, et l'ancienne Babylone, entre 2000 et 1600 avant notre ère, on savait déjà qu'un triangle inscrit dans un demi-cercle était rectangle, mais c'est à Thalès, vers –600, que l'on doit un énoncé rigoureux : tout angle inscrit dans un demi-cercle est droit. On lui attribue également la première démonstration. Cela n'étonne personne en Allemagne, où les écoliers connaissent ce résultat sous le nom de théorème de Thalès. L'historienne Pamphile d'Epidaure, qui vécut sous Néron, donc bien plus tard, relate que Thalès, complètement enthousiasmé par sa découverte, aurait sacrifié un ... Lire la suite
