
Un polygone est donc simplement une figure à plusieurs angles. Il apparaît pour la première fois sous la forme « poligone » chez Pierre Verney en 1520 dans son Succinte, briefve et compendieuse collection géométrale. On retrouve le suffixe gone dans « diagonale », un segment qui joint un sommet à un autre non voisin, en traversant (dia, « à travers ») un angle (gonos). L’utilisation de ce terme est attestée dès la fin du XIIIe siècle.
La nomenclature
Le nom d’un polygone n’est autre, en règle générale, que son « nombre d’angles » auquel on ajoute le suffixe gone.
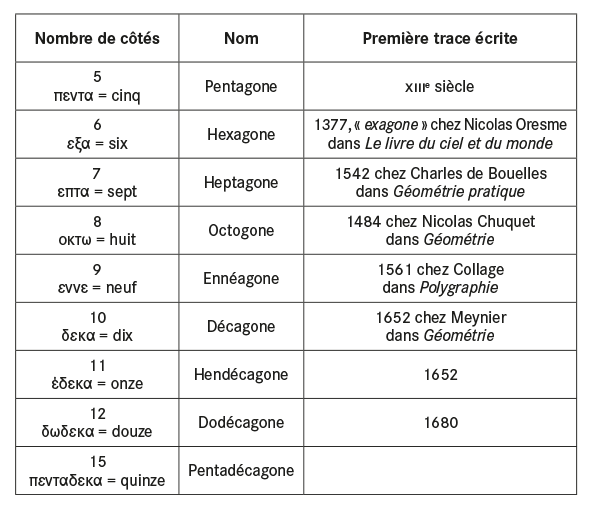
À noter que le terme « nonagone », parfois trouvé dans la littérature, est incorrect, car hybride latino-grec. On lui préférera « ennéagone » ! Après douze côtés, ce qui est assez rare, l’expression « n-gone » est souvent plus commode et plus explicite, de sorte que le cercle peut être vu comme un « infini-gone ».
Transition gréco-latine
Pour les polygones les plus courants, à trois ou quatre côtés, la nomenclature est prise au bas Moyen Âge sous un nouvel angle, à côté du grec, et devient latine avec latus (« côté ») en place de gonos (« angle »). Le nombre caractérisant le polygone ne change pas, hors sa langue, puisque, fort heureusement, le nombre d’angles d’un polygone est égal à son nombre de côtés (formule d’Euler).
Ainsi, un polygone à trois côtés est un trigone, en 1377, chez Nicolas Oresme, dans Le livre du ciel et du monde. Mais l’usage courant lui préfère « triangle », du latin triangulum, attesté dès les années 1270 dans Le Roman de la Rose de Jean de Meun, où l’on retrouve bien une figure avec trois angles.
Toujours chez Oresme (Ethique, 1370), une figure de quatre angles est un tétragone. Le terme correspondant, d’origine latine, est « quadrangle » (apparu au xiiie siècle) mais on lui préfère le terme « quadrilatère » de quadri (« quatre ») et latus (« côté ») que l’on trouve pour la première fois chez Jaques Peletier du Mans (Algèbre, 1554).
Notons que l’étoile à cinq branches se nomme « pentagramme », du grec penta (« cinq ») et gramma (« lettre »). Le terme « pentacle », quelques fois « pentalpha », quatre sommets définissant un « alpha », est un synonyme de pentagramme plutôt réservé à l’occultisme. Avec la même construction sémantique, l’hexagramme est l’étoile à six branches.
Par souci de cohérence lexicale, H.S.M. Coxeter utilise le terme « digone » pour désigner un polygone dégénéré avec deux côtés.
Référence : Centre national de ressources textuelles et lexicales (www.cnrtl.fr).
