La définition de la convexité est une notion de géométrie plus générale que le domaine des polygones. Par définition, une partie du plan est convexe si quel que soit le couple de points choisis dans cet ensemble alors le segment joignant ces deux points doit être tout entier contenu dans cette partie.
Pour s’appliquer aux polygones, l’ensemble à considérer est l’intérieur du polygone. Il faut donc qu’il possède un intérieur ! C’est pour cela que nous ne considérerons que les polygones simples (voir l'article Qu'est-ce qu'un polygone ?). Un polygone croisé est ainsi forcément non convexe.
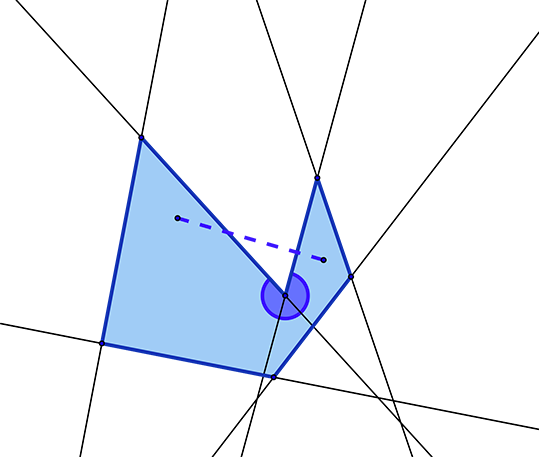
Un théorème va nous aider. Si un polygone est toujours entièrement contenu dans un demi-plan dont la frontière est une droite qui porte un côté alors il est convexe.

Un autre théorème nous indique qu’un polygone est convexe si tous ses angles internes sont inférieurs à π. Il suffit alors qu’un angle interne soit supérieur à π pour que le polygone ne soit pas convexe.