Nous verrons que tous les polygones réguliers ne sont pas constructibles à la règle et au compas, mais la plupart le sont (voir l'article Heptadécagone : le vrai et le faux). Voici quelques constructions qui permettent d’inscrire un polygone dans un cercle de centre O et de rayon R.
L’hexagone
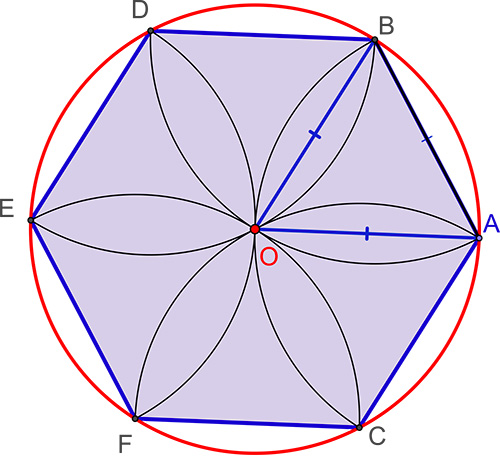
Le tracé de l’hexagone est bien connu de tous les écoliers en quête de rosaces. Il suffit de reporter le rayon du cercle pour construire un hexagone régulier. Le cercle de centre A et de rayon R coupe le cercle premier en B et C. Le triangle OAB est équilatéral. Les symétriques de A, B et C permettent d’obtenir l’hexagone ABDEFC, qui se décompose en six triangles équilatéraux.
Le triangle équilatéral
La construction du triangle équilatéral se déduit directement de la construction précédente. Pour inscrire un triangle équilatéral au cercle de centre O et de rayon R, tracez un diamètre [AB]. Le cercle de centre A et de rayon R coupe le premier cercle en C et D. Les triangles AOD et AOC sont deux des six triangles composant l’hexagone de la figure précédente. Le triangle BDC est le triangle équilatéral recherché.
