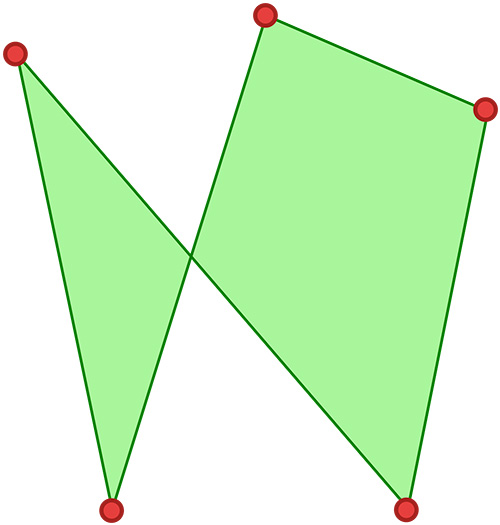
Il n’en n’est rien, mais Albert Girard explique qu’il existe trois formes de quadrilatères : « Les formes sont la simple, la croisée, & l’autre ayant l’angle renversé. » Cette classification concerne les polygones ordinaires, c’est-à-dire des polygones où un point n’appartient pas à plus de deux côtés.
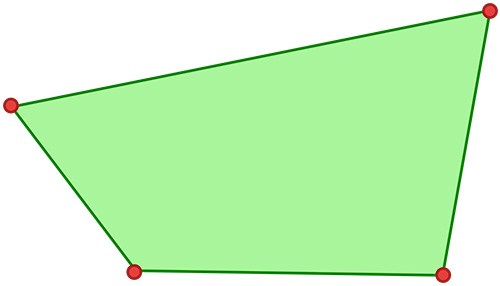
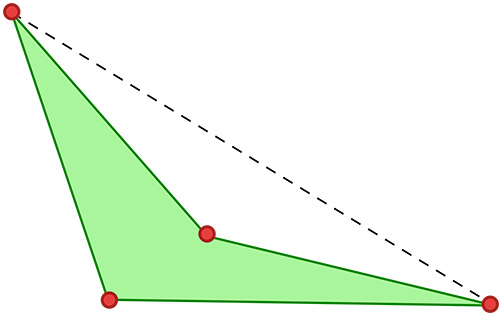
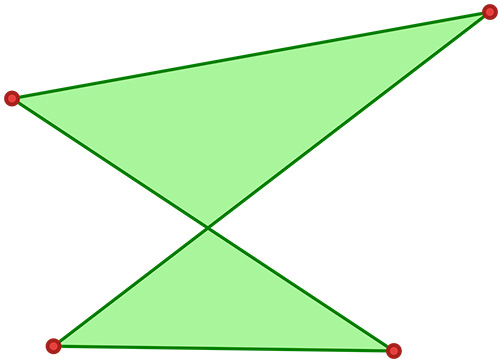
Nous voyons apparaitre la notion d’angle renversé chez Girard, c’est à dire de convexité. Dans la figure du milieu, un sommet se trouve à l’intérieur de l’enveloppe convexe du quadrilatère.
Les 11 formes du pentagone
À propos des pentagones, Girard nous affirme : « Quant aux 11 formes, il y en a 4 d’une superficie, 4 de deux, une de trois, une de 4, & une de six. » Apparemment, ce que Girand entend par « superficies » sont les domaines délimités par les arrêtes.
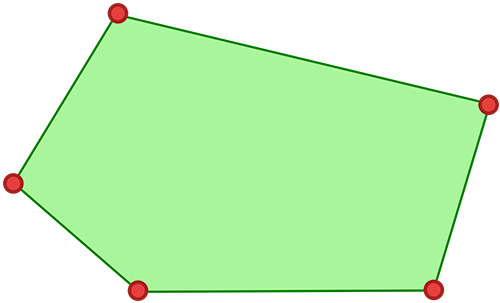
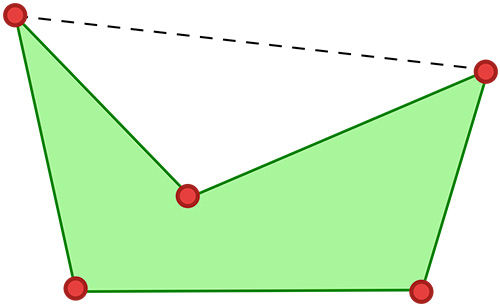
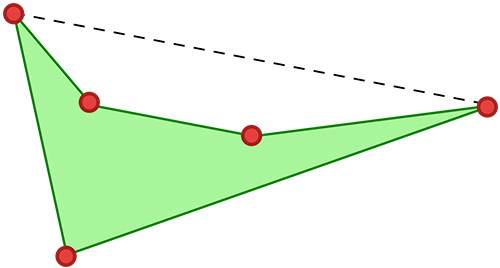
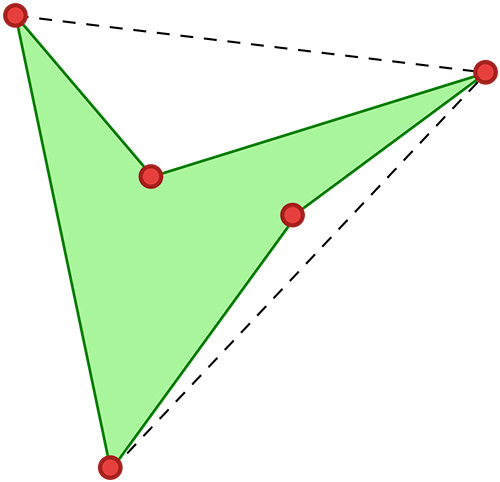
Remarquons qu’il y a d’abord un seul sommet à l’intérieur de l’enveloppe convexe puis deux. Dans un premier temps, ils sont consécutifs puis séparés par un sommet.