
Un polygone simple, ou polygone de Jordan, définit un intérieur et un extérieur (voir l'article Qu'est-ce qu'un polygone ?). Quel algorithme permet de déterminer si un point du plan est à l’intérieur ou à l’extérieur du polygone ? Voilà une question qui parait triviale pour un polygone pas trop compliqué comme sur la figure suivante :
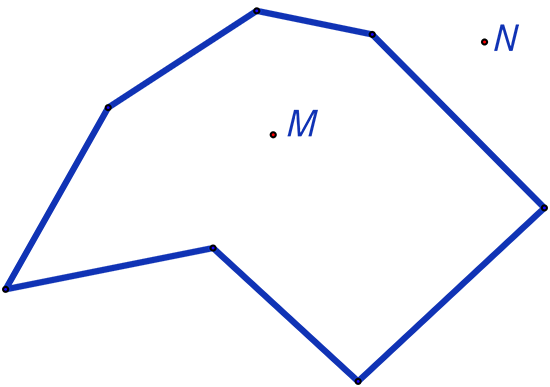
Un quart de seconde suffit, au cerveau humain, à nous dire que le point M se trouve à l’intérieur du polygone alors que le point N se trouve à l’extérieur. Mais comment faire algorithmiquement ? Cette question est récurrente dans les systèmes d’informations géographiques, les interfaces graphiques, l’infographie, les systèmes de conception assistée par ordinateur, les systèmes de robotiques. Il existe, en outre, des cas plus complexes où l’œil peut être trompé.
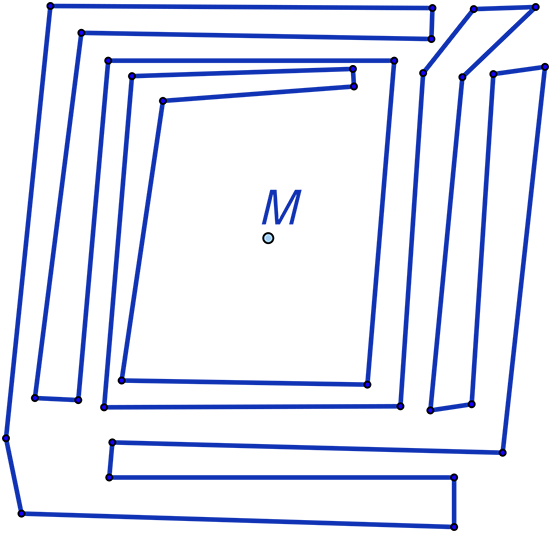
Le polygone est bien un polygone simple mais le point M est-il à l’intérieur ou à l’extérieur du polygone ?
La méthode du « croisé de rayon »
L’algorithme « point dans zone » le plus simple est le « ray crossing method », issu des travaux de Stig Nordbeck et Bengt Rystedt de 1967 en cartographie. Il consiste à faire passer une droite par le point dont on veut connaitre la position. Puis on compte le nombre d’intersections avec le polygone, en partant de l’extérieur. À chaque fois que ce nombre est impair, nous sommes à l’intérieur du polygone. L’utilisation d’une droite horizontale ou verticale permet de simplifier les calculs.
Cet algorithme est simple à implémenter. Il faut faire attention au cas où la droite passe un sommet. Si le point à identifier est très proche d’un côté, cela peut aussi être problématique. Il existe de nombreux raffinements de cet algorithme, massivement utilisé, afin d’en diminuer la complexité calculatoire.

