Un quadrilatère simple ABCD est une ligne brisée fermée joignant, dans l’ordre, les points sommets A, B, C, D et A, définissant ainsi un intérieur et un extérieur. Il est dit convexe si tout segment joignant deux quelconques de ses points est entièrement contenu dans son intérieur. On peut tout aussi bien dire que le quadrilatère est d’un même côté d’une droite définie par deux sommets consécutifs. Les parallélogrammes et trapèzes sont ainsi, dans tous les cas de figure, des exemples de quadrilatères convexes.
Quadrilatère de Pierre
Dès l’Antiquité, des théorèmes généraux ont été établis pour les polygones, principalement triangles et quadrilatères. Un des plus célèbres est certainement celui de Ptolémée caractérisant les quadrilatères inscriptibles dans un cercle (voir encadré).
Un résultat plus élémentaire fut obtenu par Pierre Varignon (1654-1722), ainsi que diverses variantes et généralisations. Considérons les points P, Q, R et S, milieux des côtés du quadrilatère ABCD.
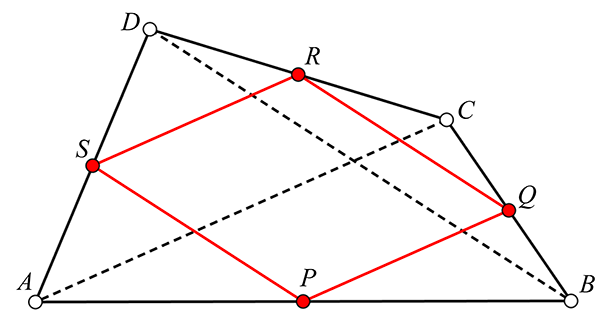
Le théorème de Varignon :
le quadrilatère PQRS est un parallélogramme.
Théorème de Ptolémée
Si le quadrilatère ABCD est inscriptible,
les angles opposés et
sont supplémentaires : α + β = π (par le ... Lire la suite
